How To Find The Final Volume Of A Gas

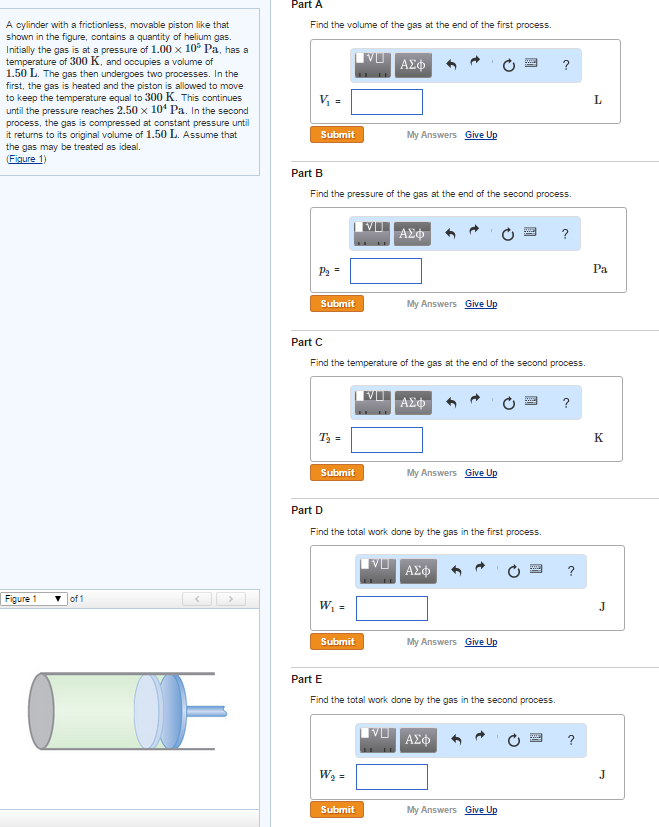
Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships , then put them together in the ideal gas law. The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law). The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law).

Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). The noble gases xenon and helium are known to possess neuroprotective properties. Xe is considered the golden standard neuroprotective gas. In contrast, He has a lower molecular weight and higher thermal conductivity and specific heat than those of nitrogen, but is unfortunately far less potent than Xe at providing neuroprotection. Therefore, combining Xe with He could allow obtaining, depending on the gas inhalation temperature and composition, gas mixtures with neutral or hypothermic properties, the latter being advantageous in term of neuroprotection. However, calculating the thermal properties of a mixture, whatever the substances – gases, metals, rubbers, etc. – is not trivial.

First, we must determine the question, which is to calculate the volume of a quantity of gas at a given temperature and pressure. In a second step, after establishing a basis, we must convert the mass of methane that will be the basis into pound moles. Third, we must convert temperature in degrees Fahrenheit into absolute degrees Rankin and, fourth, convert pressure from psig into psia.

Fifth, we must select the appropriate ideal gas constant and use it with a rewritten form of Equation 4.11 to determine the volume of 11.0 lbs of methane gas. Finally, we can substitute the values previously determined into the rewritten equation to calculate the volume. This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in .

How Do You Find The Final Volume Of A Gas An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 9.11. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter. Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures.

An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 3. Like the other ideal gas laws, Avogadro's law only approximates the behavior of real gases. Under conditions of high temperature or pressure, the law is inaccurate. The relation works best for gases held at low pressure and ordinary temperatures. Also, smaller gas particles—helium, hydrogen, and nitrogen—yield better results than larger molecules, which are more likely to interact with each other. We have just seen that the volume of a specified amount of a gas at constant pressure is proportional to the absolute temperature.

In addition, we saw that the volume of a specified amount gas at a constant temperature is also inversely proportional to its pressure. We can correctly assume that pressure of a specified amount of gas at a constant volume is proportional to its absolute temperature. Let us also add the fact that the volume at constant pressure and temperature is also proportional to the amount of gas. Similarly, the pressure at constant volume and temperature is proportional to the amount of gas. Thus, these laws and relationships can be combined to give Equation 4.10. Compressing a gas initiates changes in its characteristics.

Because you're compressing it, the volume of space the gas occupies decreases, but a lot more happens than this alone. Compression changes the temperature and pressure of the gas too, depending on the specifics of the situation. You can understand the changes that occur using an important law in physics called the ideal gas law. This law simplifies the real-life process somewhat, but it is useful in a wide range of situations.

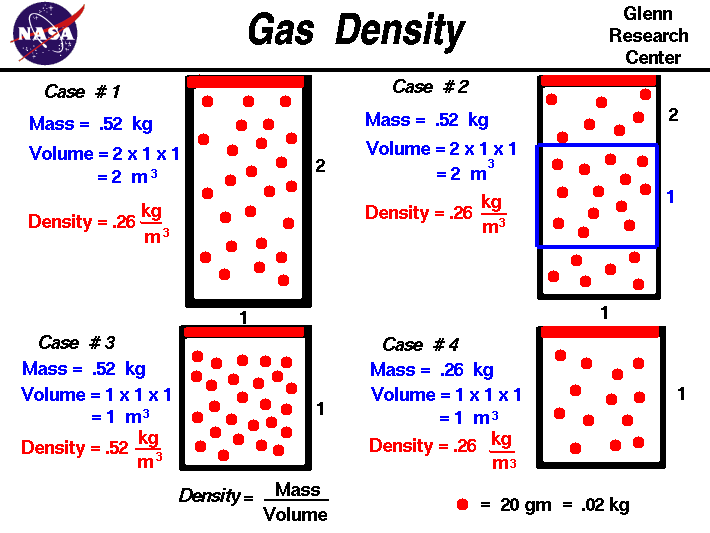
The stateof agasis defined by various propertieswhich we can observe with our senses, including the gaspressure ,temperature , mass (number of moles - m), andvolume which contains the gas. It is observed that, if we have a certain amount of gas present, the value of the temperature and pressure does not depend on the amount of gas which we examine. If we insert a plate into the tank which cuts the volume in half, the temperature in each half remains the same, as does the pressure.

The value of pressure and temperature does not depend on the amount of gas used in the measurement. The mass of the gas, on the other hand, does depend on the volume. The mass in each section of the tank is one half the mass of the entire tank. The mass depends on the volume and, in turn, the volume depends on the mass. If we maintain the pressure and temperature of this gas and fill an object which can vary its volume, like a balloon, or a cylinder with a sliding end, the final volume depends directly on the amount of the gas that we inject. Notice that if we hold the volume constant and inject mass, the value of pressure and temperature change, but in the example on this slide, the total mass is kept constant.

The attraction or repulsion between the individual gas molecules and the container are negligible. Further, for an ideal gas, the molecules are considered to be perfectly elastic and there is no internal energy loss resulting from collision between the molecules. Such ideal gases are said to obey several classical equations such as the Boyle's law, Charles's law and the ideal gas equation or the perfect gas equation. We will first discuss the behavior of ideal gases and then follow it up with the behavior of real gases.

It is possible to calculate the final volume or pressure of an ideal gas using the various gas laws such as Boyle's law. According to this particular law, the pressure is inversely proportional to the volume. The necessary condition is that temperature should be constant.

In addition, in line with its scarcity, Xe suffers an excessive cost of production that is a major obstacle to its clinical development. Avogadro's gas law states the volume of a gas is proportional to the number of moles of gas present when the temperature and pressure are held constant. This example problem demonstrates how to use Avogadro's law to determine the volume of a gas when more gas is added to the system.

In an isenthalpic process, system enthalpy is constant. In the case of free expansion for an ideal gas, there are no molecular interactions, and the temperature remains constant. For real gasses, the molecules do interact via attraction or repulsion depending on temperature and pressure, and heating or cooling does occur. For reference, the Joule–Thomson coefficient μJT for air at room temperature and sea level is 0.22 °C/bar. Depending on the units of measure for the pressure, the volume, the number of moles, and the absolute temperature, some values for the ideal gas constant R are given in Table 4.1 and Appendix C for different units-of-measure systems. If we partially fill an airtight syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C.

If we slowly push in the plunger while keeping temperature constant, the gas in the syringe is compressed into a smaller volume and its pressure increases; if we pull out the plunger, the volume increases and the pressure decreases. This example of the effect of volume on the pressure of a given amount of a confined gas is true in general. Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa. Volume-pressure data for an air sample at room temperature are graphed in . Volume-pressure data for an air sample at room temperature are graphed in Figure 9.13.

For a constant volume and amount of air, the pressure and temperature are directly proportional, provided the temperature is in kelvin. The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises. Volume-pressure data for an air sample at room temperature are graphed in Figure 5.

As a result, the highest is the volume proportion of He (Ya-Yc), the lowest is the volume proportion of Xe (Yc-Yb) in the gas mixture. However, whether body temperature as measured in rats after breathing Xe-He gas mixture would be consistent with the predictive results shown in Table 1 remains to be investigated. Also, translation to humans could need establishing new regression lines regarding the effects of Xe-O2 and He-O2 gas mixtures on body temperature. The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional.

The line stops at 111 K because methane liquefies at this temperature; when extrapolated, it intersects the graph's origin, representing a temperature of absolute zero. Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm3 when immersed in a mixture of ice and water (0.00 °C).

When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm3. Find the temperature of boiling ammonia on the kelvin and Celsius scales. In another lesson, you learned about ideal gases and the ideal gas equation. But since real gases behave similarly to ideal gases at normal temperatures and pressures, we can use the ideal gas equation to predict the behavior of real gases under these conditions.

For a gas, which variables are inversely proportional to each other if all other conditions are held constant? Where the heat capacity ratio (CP/CV) is 5/3 for a monatomic gas such as helium. Since times and lengths can be measured very accurately, the measurement of acoustic velocities by the detection of successive resonances in a cylindrical cavity appears to offer an ideal way to measure temperature. This is not completely correct, however, since boundary effects that affect the velocity of sound are important even for the simplest case in which only one mode is present in the cavity .

These effects unfortunately become larger as the pressure is reduced. An excellent theory relates the attenuation in the gas to these velocity changes, but the situation is very complex and satisfactory results are possible only with complete attention to detail. An alternative configuration uses a spherical resonator in which the acoustic motion of the gas is perpendicular to the wall, thus eliminating viscosity boundary layer effects. The most reliable recent determination of the gas constant, R, is based on very careful sound velocity measurements in argon as a function of pressure at 273.16K, using a spherical resonator.

A certain mass of gas has a volume of 1000ft3 at 60psig. If temperature is constant and the pressure increases to 120psig, what is the final volume of the gas? Kinetic particle reasoning - increasing the temperature increases the kinetic energy of the molecules giving more forceful collisions which push out the gas at constant pressure. In the past lots of measurements have been made to investigate how the pressure and volume of a given mass of vary at constant temperature and how the pressure and volume gas of a fixed mass of gas varies with temperature . This resulted in the formulation of the laws of gases described in the next section 4a. Along with how to use them in calculations and problem solving.

Under these conditions, the volume of the gas will vary inversely with the absolute pressure. This equation calculates a pressure given the corresponding elements of the equivalence; Initial pressure, Initial volume, and temperature. To calculate the final temperature T2 of the gas, use the ideal gas law. If you compress a fixed number of moles of gas, and you do this in an isothermic process , the pressure must increase to account for the smaller volume on the left of the equation. Similarly, when you cool a gas at a fixed pressure, its volume decreases – it compresses.

Let Cv and Cp denote the molar heat capacities of an ideal gas at constant volume and constant pressure respectively. The preceding example was actually a simple problem that has been made more complicated here. The simple solution can provide an estimate for Step 13 of the problem-solving technique in Chapter 1, "Introductory Concepts," in which we judge our results. First, the cracking of ethane into ethylene with the hydrogen being given off doubles the number of moles of gas.

Second, the increase of temperature, from 810°R (350°F) to 2,010°R (1,550°F), also more than doubles the volume. Thus, the volume of the gases would be about quadrupled, which approximates and confirms the 4.7 times increase in our previous calculation. Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder and its pressure is observed to decrease.

Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If we heat the sphere, the gas inside gets hotter () and the pressure increases. The procedure for constant-volume gas thermometry is very much the same as that for isotherm thermometry, but detailed bulb pressure data are taken as a function of temperature for one "filling" of the bulb at the standard temperature. To first order, pressure ratios are equal to temperature ratios, with thermodynamic temperatures calculated using known virial coefficients. If the constant-volume gas thermometer is to be used in an interpolating gas thermometer mode (as for the ITS-90), the major corrections are due to the nonideality of the gas.

Therefore, according to Charles' law for an ideal gas at constant pressure, the volume will change in the same proportion as its temperature. Thus, a 20% increase in temperature will cause a 20% increase in volume as long as the pressure does not change. Similarly, if volume is kept constant, a 20% increase in temperature will result in the same percentage in increase in gas pressure. In order to study this problem, much research work has been done. The result of this research work is a term called the compressibility factor.

This is also sometimes called the supercompressibility factor. The American Gas Association has sponsored research that defines these factors for all of the conditions to which natural gas is normally exposed. The factors have been found to be affected by temperature, pressure, gas specific gravity, and gas composition, particularly the inert content of the gas. This information is in the form of tables of values as well as the equations for calculating the factor values from the gas properties and conditions. There are a number of chemical reactions that require ammonia.

In order to carry out the reaction efficiently, we need to know how much ammonia we have for stoichiometric purposes. Using gas laws, we can determine the number of moles present in the tank if we know the volume, temperature, and pressure of the system. If we heat the sphere, the gas inside gets hotter (Figure 9.10) and the pressure increases. If we heat the sphere, the gas inside gets hotter and the pressure increases. Charles's law is an experimental gas law that describes how gases tend to expand when heated. When the pressure on a sample of a dry gas is held constant, the Kelvin temperature and the volume will be in direct proportion.

This law describes how a gas expands as the temperature increases; conversely, a decrease in temperature will lead to a decrease in volume. A gas has an initial volume of 2.4 L at a pressure of 1.5 atm and a temperature of 273 K. The pressure of the gas increases to 4.5 atm, and the temperature of the gas What is the final volume of the gas? 0.92 L 6.3 L 8.3 L Subrit Save and Exit Mark this and teturn ContentViewers/AssessmentViewer/Activit. The Peng-Robinson equation of state was used to calculate the volume of 100% methane gas as a function of pressure and temperature . This equation expresses fluid properties in terms of the critical properties and acentric factor of each species involved.

How Much Would 10000 Of Apple Stock Be Worth Today

If you receive notice that a company whose shares you own is doing a stock split, rest assured that the value of your shares won't change. Investing in the stock market has risks, but a stock split isn't generally one to lose sleep over. If you invest through a brokerage, you should automatically receive credit for extra shares after a stock split. As a bonus, you may see share prices rise after a stock split, as more investors become interested in the company's shares. That would increase your net worth and bring you a little closer to retirement readiness. So why would a company consolidate its shares with a reverse stock split?

By raising share prices, a reverse stock split may help a company meet the requirements for trading on a major exchange. If share prices dip too low, a company could be booted from an exchange and lose access to investors. A reverse stock split elevates share prices, helping a company stay listed.

On the first full trading day of GE's reverse split, shares got an approximately 8-fold pop in value. Shareholders that would hold a fractional share as a result of the reverse stock split will receive a cash payment in lieu of such fractional shares. Heck, including dividends, Visa's stock has returned 861% over the past 10 years. That beats the S&P 500's total return by nearly 490 percentage points. The US airline has rewarded investors with lavish annualized returns of 26% and several stock splits since 1972. An investment of $1,000 in the company that year would be worth just over $2.2 million (£1.5m) in 2016, not including any reinvested dividends.

It's not hard to figure out why M&T Bank stock is one of Warren Buffet's favorites. Back in 1983, 1,300 shares were priced at $1,000 (£2,400/£1.6k in today's money). Thanks to several stock splits, those 1,300 shares would have turned in 26,000 worth $3.1 million (£2.1m), even without the dividends reinvested. Several biotech companies have experienced rapid growth in the 21st century, offering investors enviable returns. Back in 2000, $1,000 would buy you in 62.5 shares in Illumina, 'the Google of genetic testing', at its IPO. Today, those 62.5 shares have multiplied to 125 worth $17,935 (£12.3k), even without dividends reinvested.

Like Microsoft, information technology firm Oracle went public in 1986 and has offered investors similar bumper returns over the years. In 1987, $1,000 would have bought 50 shares, which would have turned into 16,200 shares worth $646,542 (£442k) by 2016, even without the dividends reinvested. Notable for its many stock splits, McDonald's went public in 1965 and hasn't looked back. Back then $1,000 would have got you 44.44 shares at the IPO, which would have grown to 33,046 shares worth $4.1 million (£2.8m) by 2016, even more if you'd reinvested the dividends. Taking into account a 2-1 split in 2012, 1,449 shares bought in 1995 for just under $1,000 would now be 2,898 shares worth $435,018 (£297k). Packaging maker Bemis isn't the most glamorous of companies but its stock market performance definitely has the wow factor.

A thousand dollars invested in 1982 would have bought 1,299 shares in the company, which would have turned into 41,568 shares worth $2 million (£1.4m) by 2016. Currently America's largest provider of supplemental insurance, Aflac was the company to invest in back in 1955. Investing $1,000 would have bagged you 92 shares that year which, after stock splits and dividend bonuses, would represent a holding worth $10.9 million (£7.5m) today. Johnson & Johnson's initial public offering was way back in 1944.

Back then, a single share would have set you back $37.50, so $1,000 would have snapped up 26.67 shares. You'd have been wise to splash the cash as today your holding would comprise 66,675 shares worth $7.5 million (£5.1m) or in the tens of millions if you'd reinvested the dividends. Key to wartime logistics, Dow has experienced steady growth since the 1940s. A single share in 1940 was priced at $70, so $1,000 invested in 1940 would buy you 14.28 shares, which by 2016 have multiplied to 4,623 shares worth $243,124 (£166k). And if you'd reinvested the dividends, your holding would be in the hundreds of thousands of dollars.

Click or scroll through the most lucrative long-term stocks from the year you were born, based on an initial investment of $1,000. They arefundsthat contain stocks from different companies, but they aretradedlike single stocks on a stock market exchange. They normally try to match the returns of a market index, like the Dow Jones Industrial Average or the S&P 500, by investing in the stocks that are included in that index. In other words, an ETF's performance will normally match the performance of the stock market.

Learn which companies have produced impressive growth rates during the past decade. When Apple had its initial public offering of 4.6 million shares in December 1980, AAPL was valued at $22 per share. More than 40 out of 1,000 Apple employees become instant millionaires. As Apple's biggest shareholder, 25-year-old Steve Jobs ended the day with a net worth of $217 million. Known at the time as Flowers Industries, the American baked goods firm made its IPO in 1968.

An investment of 80 shares priced at $1,000 would be worth $140,000 (£96k) today, even more if you'd reinvested the dividends. An investor who purchased $1,000-worth of stock in Malaysia's Public Bank Berhad when it was listed in 1967 would now own 135,400 shares worth $336,000 (£230k), without dividends. A phenomenal investment, Walt Disney stock has enjoyed a compound annualized growth rate of 18% since 1948, as well as multiple stock splits and dividend payouts.

So $1,000 invested that year would be worth around $96 million (£66m) in 2016 assuming all the dividends had been reinvested. Tech stocks have been dominating the stock market for years now, and Netflix was the top-performer of the S&P 500 during the 2010s. Because many of the largest and highest-flying stocks are in the technology sector, that's helped to spur broader gains across the market. By comparison, a $500 investment in an ETF that tracks the S&P 500 would be worth about $910 today, assuming dividends were also reinvested. If you had spent $1,000 on Apple stock in 1980, you would have been able to buy about 45 shares at $22 apiece.

Apple shares have split four times since then—when a stock splits, it increases the number of shares an individual has—which puts the adjusted initial offering price at closer to 39 cents a share. Using that figure, an investment of $1,000 in Apple back in 1980 would yield close to $272,000 today. Past performance is not an indication of future results and investment returns and share prices will fluctuate on a daily basis.

Your investment may be worth more or less than your original cost when you redeem your shares. Current performance may be lower or higher than the performance data quoted. A stock split lowers the price of shares without diluting the ownership interests of shareholders. A shareholder would go from owning, say, 200 shares of $50 s to owning 400 shares of $25 shares.

If you've done the math, you'll have figured out that the total value of the shareholder's stock is the same. The shareholder isn't losing money and isn't losing market share relative to other shareholders. If the stocks pay dividends, the dividends per share will decrease by the same proportion as the price, but the total dividends earned will be unaffected. That's why, from a shareholder's perspective, a stock split is nothing to sweat. Accounting for stock splits (there have been three in Apple's history), a lone share of Apple stock purchased in 1980 would today be worth $4,502.

If one purchased $1,000 worth of Apple shares 33 years ago, that investment today would be worth $204,000. If one purchased $1,000 worth of Apple shares in June of 1997, when shares were trading as low as $3.56 a share, that investment would today be worth $632,000. British property investment firm Helical Bar has rewarded early investors with excellent returns. So $1,000 invested in 1985 would have grown to $723,000 (£494,492) by 2016.

Across the pond, you would have wanted to buy shares in a firm called Balchem, the best performer on the US stock market over the last 30 years. Its stock price has increased by 107,099% since the end of 1985. Cable TV exploded in the 70s and 80s, so it's no wonder shares in Comcast, the world's largest cable company, surged throughout this time.

And 471 shares bought for just over $1,000 in 1974 would have transformed into 72,707 shares worth $4.5 million (£3.4m) by 2016 if you'd reinvested the dividends. A classic long-term investment, Coca-Cola is renowned for offering patient investors decent returns. For instance, a $1,000 investment made in 1962 would be worth $221,445 (£152k) in 2016; even more you'd reinvested the dividends. At the time, Xerox was allowed to buy 100,000 shares of Apple at $10 a share. Considering stock splits, Xerox's initial investment of $1 million would be worth roughly $1.2 billion dollars today.

For what it's worth, the legendary investor Warren Buffett is still betting on Apple—despite his general reluctance to invest in technology companies. Buffett said back in May that his holding company, Berkshire Hathaway, has 9.8 million shares of Apple. If that's still the case, several market watchers have pointed out, the recent uptick in Apple's value means Berkshire Hathaway likely made more than $60 million off the investment in a single day last week. While the term "reverse ten-bagger" isn't in common use, it could apply to Chesapeake Energy Corporation. Shares are worth about a tenth of what they were 10 years ago, as your $1,000 would be, had you invested here. Between the financial crisis and then the massive drop in oil prices in late 2014, it really hasn't been a good decade for investors in Oklahoma City-based oil and gas producer Chesapeake Energy Corporation.

Dividend yields provide an idea of the cash dividend expected from an investment in a stock. Dividend Yields can change daily as they are based on the prior day's closing stock price. There are risks involved with dividend yield investing strategies, such as the company not paying a dividend or the dividend being far less that what is anticipated. Furthermore, dividend yield should not be relied upon solely when making a decision to invest in a stock. An investment in high yield stock and bonds involve certain risks such as market risk, price volatility, liquidity risk, and risk of default.

If a company decides for a 2-for-1 stock split, for instance, each shareholder who owned a stake prior to the split will now own twice as many shares. However, each shareholder's percentage stake in the company remains the same. While each shareholder now owns twice as many shares in the company, the company also now has twice as many shares available. The total dollar value of investors' shares also remains the same.

Because each stock was split in two, each stock's share price was also roughly divided in half. A pioneer of 3G and next-generation mobile technologies, Qualcomm made its IPO in 1991 and business has been booming ever since. If you'd held onto them, your holding would now consist of 2,254 shares worth $125,300 (£85.6k), even more if you'd reinvested the dividends. Apple shares have notched up breathtaking gains over the years. In 1976, early shareholder Ron Wayne sold stock that would be worth $35 billion (£24bn) today for a paltry $800 ($3,400/£2.3k in today's money).

And if you'd invested $1,000 at the firm's IPO in 1980, your holding would be worth $300,000 (£205k) today without the dividends reinvested. The Florida-based supermarket chain was definitely worthy of your investment cash back in 1959. Given the multitude of stock splits over the years and the company's impressive growth, a $1,000 investment made in 1959 would be worth around $4 million (£2.7m) in 2016. Big pharma firm Pfizer released 240,000 shares of common stock in 1942 – the cash generated helped fund the commercialization of penicillin.

One share cost $23.47 so if you bought $1,000-worth in 1942 it would equal 6,135 shares today worth $206,950 (£142k); more if you'd reinvested the dividends. Holding onto stocks for the long run can be highly lucrative even if you spread your risk. So $1,000 put into the S&P 500 in 1942 would offer an average annualized return of 8.9% – giving you a holding of $2.9 million (£2m) today if you'd reinvested the dividends. In fact, among the five members of the FAANG group, only Apple currently pays a dividend. It's still prudent to reinvest dividends, when possible, because it's an easy way to grow your portfolio's balance.

Many of the popular tech stocks have become synonymous with the definition of growth investing in recent years. With this strategy, investors knowingly pay a premium to buy the fastest-growing stocks because they expect these companies will continue to outpace the broader market. The trade-off, however, is that a lot of tech companies don't pay dividends. The Charles Schwab Corporation provides a full range of brokerage, banking and financial advisory services through its operating subsidiaries. Its broker-dealer subsidiary, Charles Schwab & Co., Inc. , offers investment services and products, including Schwab brokerage accounts. Its banking subsidiary, Charles Schwab Bank, SSB , provides deposit and lending services and products.

Access to Electronic Services may be limited or unavailable during periods of peak demand, market volatility, systems upgrade, maintenance, or for other reasons. On Thursday, Apple shares closed at a new all-time high of $300.35 (on a split-adjusted basis), adding $30 billion to the company's market capitalization of now $1.335 trillion. If you had bought $1,000 worth of Apple shares on January 9, 2007, the day Steve Jobs unveiled the original iPhone at MacWorld 2007, your investment would now be worth $26,103. Apple first sold shares to the public on Dec. 12, 1980, at $22 per share.

The stock has split four times -- three times at 2-for-1, and one split at 7-for-1. This means you would have received two shares for every one share, or seven shares in that one case. The waystock splitswork is that you receive more shares but the stock price is cut proportionally, so the value of your investment stays the same. For example, a $1 increase in a lower-priced stock can be negated by a $1 decrease in a much higher-priced stock, even though the lower-priced stock experienced a larger percentage change. In addition, a $1 move in the smallest component of the DJIA has the same effect as a $1 move in the largest component of the average.

The 1990s brought on rapid advances in technology along with the introduction of the dot-com era. The markets contended with the 1990 oil price shock compounded with the effects of the early 1990s recession and a brief European situation surrounding Black Wednesday. But if you're not careful, you could be betting your retirement future on the success of just a handful of companies . The last 10 years have been eventful ones for the stock market. As such, there is no shortage of stocks that have provided an excellent return on investment over the last decade.

Yet another fruitful internet-related investment opportunity, eBay went public in 1998 offering shares priced at $18 a pop. A $1,000 investment at the IPO for 55.55 shares would have grown to 7527 shares at $181,028 (£124k) by 2016, even more if you'd reinvested the dividends. Buying into the world-famous toy company would have been a shrewd plan back in 1989.

A holding of 64 shares priced at just under $1,000 would now be worth $31,481 (£21.5k) had you reinvested the dividends. A reliable investment, $1,000-worth of Proctor & Gamble shares acquired in 1981 would net you $35,000 (£24k) today if you'd reinvested the dividends – that's a return of 3,407%. Investing in the Indian stock market can pay off very nicely indeed. Buying $1,000-worth of shares in Wipro, one of India's top IT companies, back in 1980 would have increased to an eye-watering 9,600,000 shares worth $76.2 million (£52m) by 2016. Rather than just calculating the change in price, which would be about 101% in that time period, we've calculated the total return. That assumes you reinvested the dividends — a portion of a company's or fund operator's profit — you earned each quarter, which is an easy way to grow the value of your portfolio.

Let's say you want to invest in a company, but its stock price may be higher than what you want to pay. Instead of buying a whole share of stock, you can buy a fractional share, which is a "slice" of stock that represents a partial share, for as little as $5. For example, if a company's stock is selling at $1,000 a share and you were buying $200 worth of it, you would own 0.2 (20%) of a share.